-Idea: Give lab practicum challenges at the beginning of units, but do them at the end. This unit is a t-bone crash between an accelerating car and a constant speed buggy.
-Push a car across a track at a constant speed.
- What do you notice?
- Does it look constant?
- What does it sound like?
- Graph with your finger in the air: d vs. t, v vs. t, what would the motion map look like?
- What will it look and sound like now?
- Will the graphs and their lines look the same?
- Will we be able to graph it by marking every 1-5 seconds like with the buggy? I have a metronome we can use to count the seconds, lets try.
- What is I lessen the angle. Will this be different?
- What can we test? What is the relationship between position and time of a car on an angled track?
- Have students put data in a data table, motion map, and position vs. time graph.
- White boarding: We all did the same lab but why do we have different data? What's different and the same? What do the coefficients tell us? What do you notice about the dots and arrows on the motion maps?
- Summary: The distance traveled in a second increases every second because it gets faster every second as it goes down the ramp. Can we do a lab based on the velocity?
- Using the data from part 1, we will approximate the velocity by what we came up with in the previous unit on constant velocity: v = change in distance/time
- Have students extend their data table to have a column for velocity that they will calculate. There will be one less data point for this column.
- Make a velocity vs. time graph now. What time should those velocities be graphed at? The times to match those velocities should be the halfway points for those time segments.
- What is our line like now? (straight) Wow look- the coefficient this time is about double the d vs. t coefficient.
- As time increases, what happens to the velocity? Increasing in even, directly proportional increments means that it has constant acceleration.
- What do the different slopes mean? What are the slope units? Can you put it in a for every statement? If you started at rest and let it go for 1 sec, how fast would it be going? For 10 seconds? Which car has the biggest/smallest coefficients?
- Summary: Slope = acceleration = change in velocity/time
- Make a new graph now, of acceleration vs. time; and add acceleration arrows to motion maps.
- Also can try the same thing with a motion detector and see how close your numbers are to the sensor's numbers.
- What's up with the velocity and acceleration arrows being in the opposite direction? Does negative acceleration always mean slowing down? (no- #3)
- How do acceleration arrows compare to ramp direction and steepness?
- How do acceleration arrow sizes compare the the change in the velocity arrow sizes?
- On #5-6, does time up = time down?
- Each group pushes a car up a ramp, but some are sloped to the right/left and motion detectors are either to the right or left.
- sloped up to the right, motion detector right
- sloped up to the right, motion detector left
- sloped up to the left, motion detector right
- sloped up to the left, motion detector left
- Each group makes a motion map, x vs. t, v vs. t, and a vs. time graphs. Whiteboard them, then circle up.
- Compare motion maps
- All get slower then faster
- Does it stop at the top? How do you know?
- Do dots on the way up and down the track line up?
- Compare position graphs
- What does a line up/down mean?
- What does slope steepness mean?
- Compare velocity graphs
- How does the position graph match this? Use straight-edge "slope-o-meter" to follow the slope along the position curve to show how velocity changes.
- How do I tell the direction of the car?
- How do I tell the change in speed of the car?
- Compare acceleration graphs
- Why are some positive and some negative? (Which way is downhill?)
- Is this a rule? Do the incline and acceleration match?
- Does negative acceleration mean slowing down? Always? Sometimes? Never?
- Conclusion: opposite velocity/acceleration signs mean slowing; same velocity/acceleration signs mean speeding up (label the parts as pos/neg on the graph and remember "the acceleration finger dance")
- For example, If the car is: the velocity is: the acceleration is:
- -slowing positive negative
- -speeding up negative negative
- -speeding up positive positive
- -slowing negative positive
- Release a ball to roll down the ramp and onto the track. Each student draws their own motion map, position, velocity, acceleration graphs. On whiteboards, groups stack the graphs vertically so the times line up.
- Extension 1: Two balls released at the same time from different points on the ramp. What happens? Whiteboard to show what will happen to the distance between them.
- Extension 2: Release two balls form the same height, but at different times. What happens now?
-Unit 3 Worksheet 1 - Constant acceleration representations
-Stacks of Kinematic Curves Worksheet
-Then add mathematical piece for connection between the equations of all of the graphs. To make more complex graphs, make sure for these graphs that velocity is not zero at time zero (start moving before starting collecting). Also demonstrate the area under the curve is still the displacement.
-Lab Practicum: Try to get an accelerating wind-up car (or fan car) to crash with a buggy car. Students may not use a time or count during the actual test. Both cars need to start 2 meters away from the crash location.
-Inquiry Labs: What are some things that you could change to affect the acceleration of a car on a ramp? Have each group test a different relationship.
- What is the relationship between the ramp angle and the acceleration?
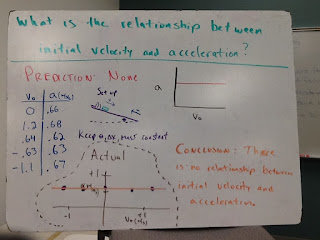
- What is the relationship between initial velocity (can change direction too) and acceleration? (no effect)
- What is the relationship between mass and acceleration? (no effect)
- What is the relationship between initial position (starting higher/lower on ramp) and acceleration? (no effect)
- White board, circle, and compare groups' data. Discuss why lines are similar but numbers are different.
- Does faster velocity mean more acceleration?
- At what angle would acceleration be greatest? (vertical)
- Have each group do multiple trials and get an average.
- Each group shares out their average.
- Does the mass or position affect the acceleration?
- Earth's free fall acceleration = 10 m/s/s! (10 is so much easier -and to ok to use- than 9.8)
- What does this mean? Make a motion map/picture. Why do the dots get further apart?
-Unit 3 Worksheet 2 - Constant acceleration representations
-Unit 3 Worksheet 4 - Constant acceleration velocity graphs and story problems












No comments:
Post a Comment